Сколько страниц найдет этот сервер по запросу кошки i собаки i лемуры

18.11.2020
0
Главная › Сколько кошки › Сколько страниц найдет этот сервер по запросу кошки i собаки i лемуры
Сколько страниц найдет этот сервер по запросу кошки i собаки i лемуры thumbnail

Содержание урока

Множества

Диаграммы Эйлера-Венна

Количество элементов во множестве

Сложные запросы в поисковых системах

Выводы

Вопросы и задания

Сложные запросы в поисковых системах

Для решения задач, в которых используются множества, например множества страниц, полученных от поисковой системы в ответ на какой-то запрос, удобно применять диаграммы Эйлера-Венна.

Задача 1. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию И, а «|» — операцию ИЛИ):

собаки | кошки 770

кошки 550

собаки & кошки 100

Сколько страниц будет найдено по запросу собаки?

Введём два множества: А — множество страниц, где есть слово «собаки», В — множество страниц со словом «кошки». По формуле, которая получена в предыдущем пункте, получаем:

NA = NA|B – NB + NA&B = 770 – 550 + 100 = 320.

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

незабудка 220

лилия & незабудка 100

лилия | незабудка 450

Сколько страниц найдёт этот сервер по запросу лилия?

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

енот 200

кашалот 300

кашалот | енот 450

Сколько страниц найдет этот сервер по запросу

кашалот & енот?

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

Италия 320

Франция 450

Франция & Италия 80

Сколько страниц найдёт этот сервер по запросу

Франция | Италия?

Рассмотрим теперь более сложную задачу с тремя областями.

Задача 2. Известно количество страниц, которые находит поисковый сервер по следующим запросам:

собаки & лемуры 320

кошки & лемуры 280

(кошки | собаки) & лемуры 430

Сколько страниц будет найдено по запросу

кошки & собаки & лемуры?

Заметим, что во всех запросах есть часть & лемуры. Это означает, что область поиска во всех случаях ограничена страницами, на которых встречается слово «лемуры».

Обозначим буквами С, К и Л области (группы страниц), содержащие ключевые слова «собаки», «кошки» и «лемуры» соответственно. Нас интересует только область, выделенная фоном на рис. 2.41, а.

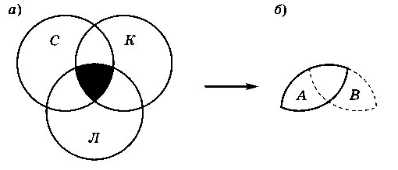
Рис. 2.41

Рис. 2.41

Эта область образована в результате пересечения двух областей (рис. 2.41, б):

А = собаки & лемуры

В = кошки & лемуры

Поэтому задачу можно свести к задаче с двумя областями.

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

А 320

В 280

А | В 430

Сколько страниц будет выдано по запросу А & В?

Используя формулу включений и исключений, полученную в предыдущем пункте, находим:

NА&B = NА + NB – NA|B = 320 + 280 – 430 = 170.

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

берёза & сирень 220

берёза & сирень & арбуз 30

сирень & (берёза | арбуз) 340

Сколько страниц найдёт этот сервер по запросу

арбуз & сирень?

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

яхта & диван 270

диван & пирог 350

яхта & диван & пирог 80

Сколько страниц найдёт этот сервер по запросу

(пирог | яхта) & диван?

Задачу с тремя областями не всегда удаётся свести к более простой задаче с двумя областями. Серьёзным упрощением может стать то, что какие-то два множества не имеют общих элементов.

Если два множества не имеют общих элементов, что можно сказать об их изображении на диаграмме Эйлера-Венна?

Задача 3. Известно количество страниц, которые находит поисковый сервер по следующим запросам:

собаки 200

кошки 250

лемуры 450

кошки | собаки 450

кошки & лемуры 40

собаки & лемуры 50

Сколько страниц найдёт этот сервер по запросу

(кошки | собаки) & лемуры?

Здесь часть & лемуры встречается не во всех запросах, поэтому свести задачу к задаче с двумя областями не удаётся. Используя те же обозначения, что и в задаче 2, построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу
(кошки I собаки) & лемуры.

На рисунке 2.42 эта область выделена фоном.

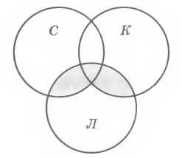
Рис. 2.42

Рис. 2.42

В общем виде задача с тремя областями очень сложна. Попробуем найти какое-нибудь упрощающее условие. Например, выделим три условия:

собаки 200

кошки 250

кошки | собаки 450

Это означает, что область кошки | собаки равна сумме областей кошки и собаки, т. е. эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит так (рис. 2.43).

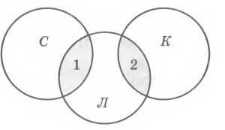
Рис. 2.43

Рис. 2.43

Размеры областей 1 (собаки & лемуры) и 2 (кошки & лемуры) нам известны, они составляют соответственно 40 и 50 страниц, поэтому по запросу

(кошки | собаки) & лемуры

поисковый сервер найдёт 40 + 50 = 90 страниц.

Известно количество страниц, которые находит поисковый сервер по следующим запросам:

солнце 230

крабы 220

лето 100

крабы | солнце 450

крабы & лето 60

солнце & лето 20

Сколько страниц найдёт этот сервер по запросу

крабы | солнце | лето?

Следующая страница Сколько страниц найдет этот сервер по запросу кошки i собаки i лемурыВыводы

Cкачать материалы урока
Сколько страниц найдет этот сервер по запросу кошки i собаки i лемуры

Источник

  • Главная
  • Вопросы & Ответы
  • Вопрос 726940
Главный Попко

более месяца назад

Просмотров : 66   
Ответов : 1   

Лучший ответ:

Сколько страниц найдет этот сервер по запросу кошки i собаки i лемуры

1) 250+200+500=950
2) 390+100=490

более месяца назад

Ваш ответ:

Комментарий должен быть минимум 20 символов

Чтобы получить баллы за ответ войди на сайт

Сколько страниц найдет этот сервер по запросу кошки i собаки i лемуры

Лучшее из галереи за : неделю   месяц   все время

Сколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемурыСколько страниц найдет этот сервер по запросу кошки i собаки i лемуры

    Сколько страниц найдет этот сервер по запросу кошки i собаки i лемуры

    Другие вопросы:

    Зачетный Опарыш

    Роль М.Н. Тухачевского в Гражданской войне ?

    более месяца назад

    Смотреть ответ  

    Просмотров : 29   
    Ответов : 1   

    Суррикат Мими

    Радиус круга равен 13 см. Значение числа π≈3,14. Определи площадь этого круга (с точностью до десятых)

    более месяца назад

    Смотреть ответ  

    Просмотров : 8   
    Ответов : 1   

    Суррикат Мими

    Хто з українців належить до насельніших людей світу?чим вони близькі до Микити Кожум`яки ?

    более месяца назад

    Смотреть ответ  

    Просмотров : 6   
    Ответов : 1   

    Мари Умняшка

    Некоторые ученные, занимающиеся экономической историей, обратили внимание, что во времена золотого стандарта новые месторождения золота открывали, как правило, после продолжительных периодов дефляции. Почему так могло случиться?

    более месяца назад

    Смотреть ответ  

    Просмотров : 59   
    Ответов : 0   

    Таня Масян

    При замыкании источника тока на внешнее сопротивление 4 ом в цепи протекает ток 0.3 а а при замыкании на сопративление 7 ом протекает ток 0,2 А​

    более месяца назад

    Смотреть ответ  

    Просмотров : 151   
    Ответов : 1   

    Источник

    Задания по теме «Представления о технических и программных средствах телекоммуникационных технологий. Интернет-технологии, способы и скоростные характеристики подключения, провайдер»

    Задание 1. Дайте определение понятия «Поисковая система»

    Задание 2. Что относится к поисковым системам общего назначения и специального?

    Задание 3. Заполните таблицу «Популярные поисковые системы»

    Задание 4. Решите задачи:

    Пример 1

    В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.

    А) Пушкин | Евгений | Онегин

    Б) Пушкин | Онегин

    В) Пушкин & Евгений & Онегин

    Г) Пушкин & Онегин

    Анализируем запросы.

    Под обозначением В) присутствует три условия, которые должны выполняться одновременно. Ясно, что таких страниц будет меньше всего. Несколько больше страниц будет найдено по запросу, в котором должны выполняться одновременно два условия – это запрос Г). Еще больше страниц найдется по условию Б), где ищется одно слово из двух возможных (логическое «ИЛИ»). И, наконец, наибольшее число страниц будет найдено по запросу А), где количество найденных страниц будет самым большим. Ответ: ГБА

    Задачи.

    1. А) Рим & Париж & Лондон

    Б) Лондон | Рим

    В) Рим & Лондон

    Г) Рим | Париж | Лондон

    2. А) ядро

    Б) ядро & атом

    В) ядро & атом & формула

    Г) ядро | атом

    3. А) литература | история | экзамен

    Б) экзамен & литература

    В) экзамен | история

    Г) история & литература & экзамен

    Пример2. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию «И», «|» – операцию «ИЛИ»):

    собаки | кошки

    770

    кошки

    550

    собаки & кошки

    100

    Сколько страниц будет выдано по запросу собаки?

    Сначала попробуем рассмотреть задачу в общем виде и вывести формулу для ее решения. Построим диаграмму с двумя областями А и В. Эти области могут быть разделены (рис. 1, а) или пересекаться (рис. 1, б).

    Рис. 1 а Рис. 1 б

    Обозначим через NX число страниц, которые выдаются по запросу Х. В первом случае, когда области не пересекаются, получаем очевидную формулу: NA|B = NA + NB. Это значит, что количество страниц, полученных по запросу A | B, будет равно сумме результатов по отдельным запросам.

    Во втором случае (рис. 1, б) сумма NA + NB дважды включает общую область, т. е. результат запроса A&B. Поэтому формула изменяется:

    NA|B = NA + NB – NA&B.

    Это более общий случай, справедливый и для рис. 1, а, где NA&B = 0. Для нашей задачи (область А – собаки, область В – кошки) получаем:

    NA|B = NA + NB – NA&B = 770 – 550 +100 = 320.

    Пример 3. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию «И», а «|» – операцию «ИЛИ»):

    собаки

    200

    кошки

    250

    лемуры

    450

    кошки | собаки

    450

    кошки & лемуры

    40

    собаки & лемуры

    50

    Сколько страниц найдет этот сервер по запросу (кошки | собаки) & лемуры?

    Обозначим буквами С, К и Л области (группы сайтов), содержащие ключевые слова «собаки», «кошки» и «лемуры» соответственно (рис. 3.17). Построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу (кошки | собаки) & лемуры.

    На рисунке 3.17 эта область закрашена серым цветом.

    В общем виде задача очень сложна. Попробуем найти какое-нибудь упрощающее условие. Например, выделим три условия:

    собаки

    200

    кошки

    250

    кошки | собаки

    450

    Это означает, что область «кошки ИЛИ собаки» равна сумме областей «кошки» и «собаки», т.е. эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит, как показано на рис. 3.18.

    Области 1 (собаки & лемуры) и 2 (кошки & лемуры) нам известны, они составляют соответственно 40 и 50 страниц, поэтому по запросу (кошки | собаки) & лемуры исковый сервер выдаст 40+50 = 90 страниц.

    Задачи:

    № 1. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

    Найдено страниц (в тысячах)

    ЗУБР & ТУР

    5 000

    ЗУБР

    18 000

    ТУР

    12 000

    Какое количество страниц (в тысячах) будет найдено по запросу ЗУБР | ТУР?

    Решите задачу, используя круги Эйлера:

    № 2. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

    Найдено страниц (в тысячах)

    ФУТБОЛ | ХОККЕЙ

    20 000

    ФУТБОЛ

    14 000

    ХОККЕЙ

    16 000

    Какое количество страниц (в тысячах) будет найдено по запросу ФУТБОЛ & ХОККЕЙ?

    Решите задачу, используя круги Эйлера:

    Пример 4. Приведено несколько запросов к поисковому серверу:

    а) лиса & енот

    б) лиса & енот & заяц

    в) лиса

    г) лиса | заяц

    Изобразите графически количество страниц, которые найдет поисковый сервер по каждому запросу.

    Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

    Задача 3. Приведено несколько запросов к поисковому серверу:

    а) (вальс & танго) | квикстеп

    б) вальс & танго & квикстеп

    в) танго & квикстеп

    г) вальс | танго | квикстеп

    Изобразите графически количество страниц, которые найдет поисковый сервер по каждому запросу.

    Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

    Пример. Адрес некоторого документа в сети Интернет

    ftp: //ict.edu/help.doc

    Запишите фрагменты адреса, соответствующие следующим частям:

    Название протокола

    ftp: //

    Доменное имя сервера

    ict.edu/

    Имя файла

    help.doc

    Задача 4.

    Адрес некоторого документа в сети Интернет

    ftp: //rnd.edu/html.doc

    Запишите фрагменты адреса, соответствующие следующим частям:

    Название протокола

    Доменное имя сервера

    Имя файла

    Источник

    Предыдущая статья
    Азиатская леопардовая кошка сколько стоит
    Следующая статья
    Какая порода кошек самая хорошая для детей
    © Заметки ветеринара Альберто Альреко